¿Qué sabemos (y qué no sabemos) sobre el confinamiento?
Un viaje al fenómeno del confinamiento y a las profundidades de la materia
Nelson Lachini (fellow de EuroPLEx, Universidad de Edimburgo)
¿Se han preguntado alguna vez qué hay dentro de un átomo?

Concepción artística de la estructura interna del protón (fuente: Brookhaven National Laboratory)
Comenzamos nuestro viaje por los misterios de la materia en 1897, cuando Joseph Thomson descubrió el electrón. Una década más tarde, Ernest Rutherford comprendió los patrones inesperados que aparecían en medidas de colisiones de partículas, con su propuesta de una estructura diminuta pero muy masiva en el corazón del átomo: el núcleo. Otra década más, y el mismo Rutherford observó el protón, responsable de dar al núcleo su carga eléctrica positiva. El protón fue el principio de una cascada de descubrimientos durante el siglo XX: el neutrón, el pion, el kaón, y cientos de partículas más, todas ellas conocidas como hadrones.
La búsqueda de objetos elementales ha sido la filosofía de la física de partículas desde sus inicios. Sin embargo, hay un fenómeno intrincado que hace muy complicado entender el mundo a distancias menores que una milbillonésima de metro: este fenómeno se llama confinamiento, y es importante por al menos dos razones. Sin confinamiento, la materia del Universo simplemente no existiría como la conocemos. Pero además, los mecanismos del confinamiento han sido un misterio que ha mantenido ocupados a físicos y matemáticos desde la formulación del problema: de hecho, hay un premio de un millón de dólares esperando a quien demuestre matemáticamente una versión simplificada del mismo.
Supongamos que tratamos de aplicar el método de Rutherford a los hadrones. Tras preparar un dispositivo experimental muy delicado, conseguimos por fin hacer chocar, por ejemplo, dos protones. Lo que vemos no tiene nada de simple: del punto de colisión surgen una multitud de hadrones y de otras partículas, como electrones y muones, pero no conseguimos ver buenos candidatos para los objetos constituyentes de los protones originales. En la década de 1970 se formuló la Cromodinámica Cuántica (QCD, por sus siglas en inglés), que propone que los hadrones están constituidos por partículas aún más pequeñas llamadas quarks y gluones. Estas partículas siempre estarían conspirando para no ser identificadas: de alguna forma, permanecerían confinadas dentro de los hadrones.
El fenómeno del confinamiento es parte de un proceso de descubrimiento gradual e interdisciplinar. Hoy en día, con los datos de los colisionadores de partículas y las predicciones teóricas obtenidas con simulaciones en superordenadores, tenemos evidencia contundente de que el confinamiento está gobernado por QCD y de que entendemos sus mecanismos básicos. A cierta distancia, pero no por separado, los matemáticos todavía intentan mostrar que el concepto se puede definir de manera rigurosa. De hecho, el confinamiento es uno de los conceptos centrales de la física de partículas, y resulta crucial para comprender las interacciones subnucleares, además de ser un problema abierto de las matemáticas puras.
Los colisionadores
Las personas apasionadas por la física de partículas probablemente conocen el Modelo Estándar, y saben de la posibilidad de encontrar física más allá del mismo, que motiva los grandes experimentos encabezados por el Gran Colisionador de Hadrones (LHC), al que se unen muchos otros como, por ejemplo, el experimento GlueX en JLab. El Modelo Estándar describe con gran éxito, y en un amplio rango de energías, una inmensa cantidad de fenómenos observados en esos experimentos, en los que participan las interacciones fuerte, débil y electromagnética. Sin embargo, en los miles de millones de sucesos catalogados en los colisionadores, nunca hemos podido capturar un quark: sólo hadrones y muchas otras partículas “carentes de quarks”.

Experimento GlueX en JLab (fuente: Wikipedia)
Por supuesto, cabe preguntarse cómo sabemos que los quarks realmente están ahí, y que el confinamiento no es simplemente una mala excusa para su no-existencia. De hecho, hacia 1970, antes del desarrollo de QCD, el modelo quark se consideraba una imagen matemática de lo que sucedía en el interior de los piones y otros hadrones, pero no una descripción directa en términos de objetos físicos. Aunque no es necesario entrar en cuestiones filosóficas de la física moderna: simplemente, los quarks no eran tomados completamente en serio por la comunidad científica.
Pero pronto nació QCD, y al hacerlo puso quarks y gluones en el entramado matemáticamente consistente de las teorías gauge. Lo que se pensaba por aquel entonces de la teoría cuántica de campos predecía que los quarks podrían ser aislados en los colisionadores; pero han pasado muchos años, y, aunque tenemos una evidencia experimental abrumadora de que QCD funciona, seguimos sin una detección directa de los quarks.
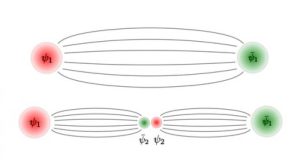
Ejemplo de rotura de una cuerda: un par quark-antiquark se convierte en dos.
Uno de los mecanismos dinámicos más conspicuos de entre los que forman parte del confinamiento es la llamada “rotura de la cuerda”, cuando los “tubos” de campo cromoeléctrico que unen los quarks entre sí se estiran hasta partirse. Para entender el proceso, imaginemos el enlace entre un quark y un antiquark como una “cuerda” elástica (esta es una descripción cruda del tipo de hadrón que conocemos como “mesón”: por ejemplo, piones o kaones). Para hacernos una idea de las magnitudes involucradas: la tensión de esta cuerda es tal que podría soportar el peso de varios coches estirándose apenas una milbillonésima de metro. Si queremos separar el quark del antiquark, tenemos que aplicar energía al sistema para estirar más y más la cuerda, intentando romperla; pero, debido a la enorme magnitud de su tensión, la energía necesaria es suficiente para crear un nuevo par quark-antiquark, a través de la celebérrima equivalencia masa-energía E=mc2. El quark y el antiquark así formados se unen inmediatamente a los preexistentes, y donde empezamos con un mesón ahora tenemos dos. Y todo esto ocurre a distancias tan pequeñas (precisamente del tamaño del hadrón) que es técnicamente imposible resolver el proceso en términos de sus constituyentes en un experimento. De hecho, lo que observamos a menudo en las colisiones es el resultado de una cadena de roturas de cuerdas, a través de las cuales la energía de la colisión se almacena en la creación de chorros (jets) de hadrones que surgen del punto de interacción. La física de jets es un campo bien establecido de la física de partículas, cuyos principios básicos están encerrados en el mecanismo de rotura de la cuerda: la estructura, propiedades y composición de los jets permiten deducir información sobre los procesos microscópicos que los originan. Este es un ejemplo de cómo obtener información fenomenológica sobre el confinamiento directamente de los experimentos.
Los superordenadores
Más allá de las pruebas experimentales, las evidencias más fuertes de que el confinamiento emerge de la QCD provienen del campo que constituye uno de los pilares de EuroPLEx: la formulación de la QCD en una red espaciotemporal, llamada “lattice QCD”. En 1974, Kenneth G. Wilson, en su artículo “Confinamiento de los quarks”, desarrolló un modo para tratar el confinamiento desde el punto de vista teórico, usando una cantidad que hoy conocemos como “lazo de Wilson” (en inglés, “Wilson loop”). En el mismo artículo, Wilson dio a luz a las teorías gauge en la red, lo que a su vez permitió comenzar a simular QCD en ordenadores.
Cuando colocamos la QCD en una red finita, esto discretiza la teoría, que queda inmediatamente bien definida. Además, en general los métodos de lattice QCD no presuponen que los campos cuánticos sean excitados débilmente; esto nos permite acceder a fenómenos con interacciones fuertes entre los campos. En particular, un ejemplo paradigmático es la obtención del espectro de masas hadrónicas a partir de lattice QCD.
Tomando el trabajo de Wilson como punto de partida, las bases de la lattice QCD se desarrollaron en paralelo al incremento de la capacidad computacional en todo el mundo. Hasta los años 1990 era muy difícil simular la QCD con todos sus ingredientes, en particular permitiendo las interacciones de quarks que aparecen y desaparecen en el vacío cuántico. En consecuencia, las simulaciones predecían el espectro hadrónico con errores sistemáticos difíciles de controlar.
En los 2000s, con el aumento de potencia de los superordenadores pero, sobre todo, gracias al desarrollo de nuevos algoritmos, la física teórica produjo las primeras simulaciones realistas de QCD con quarks dinámicos, y con ellas los primeros cálculos del espectro hadrónico desde primeros principios: y, en efecto, las masas simuladas (puntos rojos) se ajustan muy bien a las medidas experimentales (líneas oscuras).
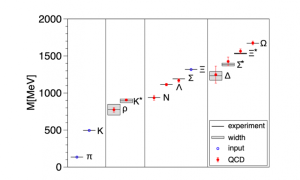
Espectro de hadrones (fuente: BMW Collaboration, https://arxiv.org/pdf/0906.3599.pdf)
La manera en que los hadrones adquieren sus masas es un efecto llamado “generación dinámica de masa”, un mecanismo no trivial asociado al confinamiento. Este es un ejemplo del tipo de confirmación convincente de la emergencia del confinamiento de la QCD. De hecho, las simulaciones de lattice QCD permiten calcular directamente la energía de ligadura entre quarks y antiquarks, que resulta crecer linealmente con la distancia entre ellos. Dicho comportamiento lineal es característico de una cuerda que se estira, lo que encaja con la visión del confinamiento en términos de tubos de flujo que evocamos antes. Las simulaciones con quarks dinámicos van más allá, y demuestran que QCD da lugar a la rotura de la cuerda, otra evidencia positiva del confinamiento.
Otro aspecto del problema es el llamado confinamiento del color. En QCD la interacción fuerte está gobernada por el intercambio de cargas de color (de ahí el prefijo “cromo”), análogas a la carga eléctrica en electromagnetismo. Los gluones y los quarks poseen carga de color, y decimos que son coloreados. El confinamiento del color es una consecuencia directa de las propiedades de simetría de la QCD, y supone que no sólo los quarks, sino cualquier otro estado coloreado (gluones, o cualquier partícula compuesta que no es “blanca”, de color neutro) es inobservable en un detector.
La búsqueda de partículas compuestas principalmente por gluones, en experimentos y en simulaciones, es otra rama de investigación que ayuda a revelar los mecanismos del confinamiento. Estas partículas, llamadas “glueballs” (un juego de palabras entre “bolas de gluones” y “bolas de pegamento”, que podríamos jocosamente traducir como “pegabolas”), son estados ligados masivos predichos por las simulaciones en la red desde los 1980s. Este tipo de partícula es teóricamente detectable, pero es también altamente inestable y se mezcla cuánticamente con otros hadrones, lo que plantea serias dificultades prácticas a los experimentos. Recientemente se han anunciado indicaciones sólidas de que el odderon, una glueball con un número impar de gluones, ha sido observada en el LHC y en antiguos datos de Tevatron, el acelerador (ya fuera de uso) del Laboratorio Nacional Fermi en las afueras de Chicago. Es importante advertir que los gluones no tienen masa: las glueballs son estados puramente de interacción fuerte, y toda su masa está almacenada en los tubos cromoeléctricos que mantienen unidos los gluones constituyentes.
Además de esta abundante evidencia experimental y numérica, se ha invertido mucho trabajo en tratar de comprender el confinamiento en términos de mecanismos concretos relativamente simples, desde varios puntos de vista: superconductividad dual, monopolos, vórtices de centro de grupo, … Todas ellas proporcionan descripciones adecuadas del confinamiento hasta cierto punto, ya que permiten reproducir muchas de sus características (por ejemplo, la rotura de la cuerda), pero también en todas ellas han sido halladas limitaciones. Estos modelos no están necesariamente conectados a la QCD de manera directa, sino que son intentos de describir el confinamiento a través de mecanismos efectivos, usando tanto simulaciones como cálculos analíticos. Se espera que en el futuro sea posible obtener alguno de ellos directamente a partir de la QCD, y explicar cómo emerge de la misma, lo que proporcionaría una mejor comprensión teórica de este enrevesado fenómeno.
El premio
Hasta ahora hemos contemplado el confinamiento desde el punto de vista de la Física. Otra manera de pensar en ello proviene de la matemática pura. En 2000, el Clay Mathematics Institute estableció los siete Millennium Prize Problems, partiendo de las sugerencias de especialistas en matemáticas y física teórica. Uno de estos famosos siete problemas está de hecho relacionado con el confinamiento: probar rigurosamente que una de sus propiedades claves, la generación dinámica de masa, tiene lugar en una versión simplificada de QCD, en la que sólo hay gluones pero no quarks dinámicos (la llamada teoría de Yang-Mills). Por supuesto, cualquier prueba recibirá un escrutinio riguroso, y sólo después de haber sido cuidadosamente validada por pares se tendría derecho al premio. De los siete problemas, el único que ha sido resuelto hasta ahora es la llamada Conjetura de Poincaré, demostrada por Grigory Perelman en 2003. El Clay Institute reconoció la validez de la prueba en 2006; pero, curiosamente, Perelman rechazó el premio.
Sin embargo, el asunto es que estamos hablando de un tipo específico de “explicación” matemática: proponer un conjunto de axiomas y demostrar sus consecuencias. Aunque podemos decir mucho sobre las teorías cuánticas de campos en espacios-tiempo continuos a varios niveles de rigor matemático, no hemos formulado axiomáticamente la QCD realista ni su versión sin quarks, que son los pasos necesarios para ganar el premio. Por supuesto, esto no nos impide hacer predicciones muy concretas utilizando la QCD y comparándola con los resultados experimentales, lo más probable es que las matemáticas aún estén alcanzando a la física, como ha ocurrido con frecuencia en la historia.
Todo comenzó con la propuesta, y con la observación empírica, de que los quarks no podían ser aislados colisionando hadrones. El avance de las técnicas computacionales nos ha proporcionado evidencias fuertes de que QCD no sólo necesita los quarks y los gluones como elementos básicos, sino que también predice su carácter esquivo. El confinamiento es un fenómeno extremadamente rico, con un papel central en la descripción de las interacciones fuertes, y da lugar a preguntas muy profundas en física teórica y experimental, pero también en matemáticas puras.
Claramente, el tipo de preguntas que se plantean en física y en matemáticas son diferentes. Demostrar rigurosamente la existencia de una teoría es fundamental en matemática, pero a pesar de la ausencia de este requisito la comunidad de física teórica ha establecido un altísimo nivel de confianza en la QCD y en la realidad del confinamiento sobre la base de las simulaciones y de los tests de alta precisión realizados en experimentos. En cualquier caso, la comunidad científica recibiría con enorme interés una prueba matemática del confinamiento, sobre todo porque probablemente estaría acompañada por un conjunto de herramientas muy útil para avanzar hacia la física más allá del Modelo Estándar.
Referencias:
Artículo sobre GlueX en wikipedia.
Ab-initio Determination of Light Hadron Masses (BMW Collaboration)
Artículo del CERN Courier sobre el descubrimiento del odderon.
Este post fue publicado originalmente en blog QuarkBits por SciLogs-Blogs de ciencia de Investigación y Ciencia.

