¿Está el magnetismo del muon desvelando física más allá del Modelo Estándar?
La física de partículas de alta precisión se enfrenta a una de las aventuras más fascinantes de las últimas décadas.
Lucius Bushnaq (fellow de EuroPLEx, Trinity College Dublin)
El pasado 7 de abril, el Fermi National Accelerator Laboratory (Fermilab), en las afueras de Chicago, anunció una nueva medida del momento magnético del muon. El resultado ha confirmado la discrepancia con la predicción teórica, en pie desde hace casi dos décadas, y que ahora mismo se sitúa en 4.2 desviaciones estándar. Esto sugeriría inmediatamente la posibilidad de nueva física, fuera de los límites del Modelo Estándar de la física de partículas; sin embargo, un nuevo cálculo teórico, publicado el mismo día del anuncio, ha alargado mucho la sombra de la duda.

El experimento g-2, en Fermilab. [fuente: Fermilab]
En nuestro actual modelo de la física, el muon es una partícula elemental; es decir, es una de las piezas fundamentales del Universo tal como lo entendemos. El muon es una partícula muy parecida al electrón: tienen la misma carga eléctrica y el mismo spin cuántico (una suerte de momento angular intrínseco); pero pesa unas doscientas veces más que el electrón. También es inestable: un muon en reposo se desintegra en otros partículas en apenas unos microsegundos.
El momento magnético del muon lleva tiempo siendo objeto de atención. Hace unas dos décadas, un experimento del Brookhaven National Laboratory (BNL) realizó una medida de esta cantidad con una precisión nunca vista hasta entonces, y halló una discrepancia entre el resultado y la predicción de nuestro modelo fundamental de la física de partículas, el Modelo Estándar.
La búsqueda de nueva física fundamental tiene lugar, a grandes rasgos, de dos maneras distintas. En las búsquedas directas, como las que lleva a cabo el Large Hadron Collider, se aceleran y hacen colisionar haces de partículas a energías inmensas. Como la masa es energía, esto permite la creación temporal de partículas muy pesadas e inestables, que potencialmente estarán más allá del rango de energía descrito por nuestros modelos actuales. Esta fue, por ejemplo, la manera en que se descubrió el bosón de Higgs.
El segundo camino es el de las medidas de altísima precisión. En teoría cuántica de campos, el mundo está descrito por diferentes tipos de campos cuánticos, correspondientes a otras tantas partículas elementales. Todos estos campos interactúan a través de acoplamientos, bien directos, bien indirectos, de modo que la mera existencia de un nuevo tipo de campo influenciaría el comportamiento de los demás, incluso a escalas de energía considerablemente más bajas que aquellas a las que se podría producir directamente la nueva partícula asociada. Al tratarse de un efecto indirecto, su impacto sobre las cantidades observables es generalmente pequeño, de modo que es necesario realizar medidas muy precisas para detectarlo. Si el resultado de una de estas medidas de precisión discrepa de forma significativa del Modelo Estándar, podríamos estar ante la huella de una nueva partícula. Algunas cantidades son más sensibles que otras a estos efectos, o bien es posible medirlas con una precisión tan alta que permitirían desenterrar incluso un efecto diminuto. El momento magnético del muon pertenece a esta segunda categoría, por lo que el resultado de BNL inmediatamente atrajo mucho interés.
Las medidas experimentales siempre son obtenidas con una cierta incertidumbre – o, en la jerga habitual, “error”. Pero también las cantidades teóricas están afectadas por incertidumbres: el cálculo de cantidades físicas en teoría cuántica de campos puede, por ejemplo, requerir que parte del cálculo sea realizada numéricamente y por ello con precisión limitada, o bien, como veremos en el caso que nos ocupa, utiliza en parte resultados experimentales que se saben bien descritos por la teoría. La diferencia entre el error de la medida de BNL y el mejor cálculo teórico disponible en aquel momento era de alrededor de 3 desviaciones estándar cuando se combinaban los errores del experimento y la teoría, lo que corresponde a una probabilidad 1/400 de que el efecto se debiera a una fluctuación estadística; claro está, en el caso de que no hubiera nueva física involucrada. Sin embargo, el umbral convencionalmente aceptado para anunciar un nuevo descubrimiento en física de partículas es de cinco desviaciones estándar, correspondientes a una probabilidad 1/1500000 de que el resultado ocurra por casualidad si la hipótesis nula es correcta. De modo que, sea para confirmar el descubrimiento de nueva física, sea para refutar la anomalía como un artefacto estadístico, era necesario aumentar la precisión tanto del resultado experimental como de la predicción teórica.

El anillo, transportado por la gabarra Miss Katie, remonta el Mississippi y pasa frente al Gateway Arch en St Louis. [fuente: Fermilab]
En el lado experimental, la propuesta fue repetir un experimento muy similar al de BNL en Fermilab. De hecho, el dispositivo usa exactamente el mismo anillo de almacenamiento superconductor, de 15 metros de diámetro y 700 toneladas de peso, que fue transportado entre los dos laboratorios por medio de barcazas y camiones. En Fermilab es posible inyectar un haz de muones ultrarrelativistas mucho más intenso que el disponible en BNL, lo que, unido a un sistema de detectores más avanzado, permite aumentar la precisión de la medida. Al girar en el campo magnético generado por el anillo el spin de los muones experimenta una ligera precesión, similar a la del eje de una peonza que gira, con el campo magnético en el mismo papel para el muon que el que tiene el campo gravitatorio para la peonza. Al medir la frecuencia de la precesión, es posible determinar el momento magnético del muon con una precisión exquisita.
El resultado de Fermilab anunciado el 7 de abril corresponde al primer periodo de toma de datos del experimento, que finalizó hace más de dos años. Ahora mismo se están analizando los datos tomados en los dos periodos sucesivos, y está previsto que el resultado sea anunciado en verano de 2022. Con el primer conjunto de datos, la precisión ha resultado ser similar a la del valor final de BNL, obtenido tras varios años de medidas, y el valor es perfectamente consistente con el ya conocido. Tomando la media de ambos, el llamado factor giromagnético del muon – es decir, el momento magnético en unidades del magnetón de Bohr, comúnmente llamado “g” – resulta ser 2.00233184122(82), donde el número entre paréntesis representa la incertidumbre, al nivel de una desviación estándar, de las dos últimas cifras significativas. La impresionante precisión de esta medida es de cuatro partes en mil millones. El objetivo final del grupo de Fermilab, cuando se hayan apurado todos los periodos de toma de datos, es disminuir este error por un factor 4.
La cercanía del valor medido a 2 no es casual: como explicamos en otro post de este mismo blog, la unión de la mecánica cuántica y la relatividad especial en la ecuación de Dirac predijo g=2 ya en 1928. La desviación del valor exacto se debe a las interacciones del muon con el vacío cuántico, en el que bullen todas las demás partículas del Modelo Estándar en una perpetua danza de creación y aniquilación. Es por esto que, en los ambientes técnicos, se habla más a menudo no directamente de g, sino de la diferencia g-2, o de la cantidad a=(g-2)/2, llamada momento magnético anómalo. En el caso del muon, por lo tanto, la desviación se puede cuantificar como aμ=0.00116592061(41).
Esto nos lleva, precisamente, a discutir la predicción teórica. También en este caso la incertidumbre ha disminuido desde la época del primer resultado de BNL, y el resultado actual es 2.00233183620(86) – o, equivalentemente, aμ=0.00116591810(43). Esto es lo que da lugar a la discrepancia actual de 4.2 desviaciones estándar.
La mayor parte del error proviene de los efectos más difíciles de calcular: las llamadas contribuciones hadrónicas, causadas por las interacciones con los campos de quarks y gluones (los bosones mediadores de la interacción fuerte) del vacío. En particular, la contribución llamada “polarización hadrónica del vacío” (HVP, por sus siglas en inglés) es responsable de casi todo ese error. Y aquí es donde comienzan a aparecer sutilezas, ya que hay dos maneras de calcular la contribución HVP que parecen no estar completamente de acuerdo.
La primera manera de realizar el cálculo es no hacerlo: usando un truco matemático, la HVP puede ser relacionada con una cantidad experimental totalmente distinta (la fracción de los productos de aniquilación de electrones y positrones que forman estados ligados de quarks y gluones). Usando las medidas de dicha fracción realizadas por muchos colisionadores electrón-positrón desde los años 1960, es posible determinar la contribución HVP al momento magnético del muon. Este método, llamado “data-driven” en la literatura especializada, sigue siendo considerado la manera más precisa y fiable de calcular la HVP, y por lo tanto es tomado como “patrón oro”. De hecho, el valor teórico del momento magnético que citábamos antes proviene de aquí. Por supuesto, hay un problema potencial en el hecho de que la predicción no se lleve a cabo de manera puramente teórica: si hubiera también efectos de nueva física en los datos de aniquilación electrón-positrón, esta podría contaminar la predicción teórica.
En los últimos años, una segunda forma de determinar la contribución HVP se ha vuelto poco a poco competitiva: el cálculo directo en el Modelo Estándar usando la QCD en la red (Lattice QCD). Esta técnica, la única completamente de primeros principios para tratar la interacción fuerte, parte de la discretización del espaciotiempo, lo que permite calcular numéricamente cantidades como la contribución HVP usando algunos de los superordenadores más potentes del mundo, como ya explicamos en otra entrada del blog. De hecho, los cálculos de la HVP en Lattice QCD tienen una larga historia, pero sólo en los últimos 3-4 años han alcanzado precisiones comparables a las del método data-driven, gracias a las mejoras en los algoritmos de cálculo, a las técnicas de teoría de campos empleadas, y al permanente aumento de la capacidad computacional.
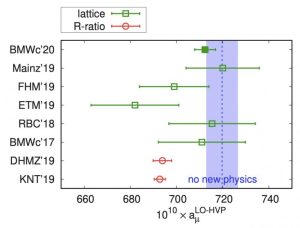
Comparación de la contribución HVP obtenida a partir de la medida experimental del momento magnético del muon (banda azul), y predicciones teóricas basadas en los métodos data-driven (puntos rojos) y Lattice QCD (puntos verdes). [fuente: Colaboración BMW]
El primer, y hasta ahora único, resultado de Lattice QCD con un error grosso modo similar al del método data-driven es el obtenido por la colaboración Budapest-Marsella-Wuppertal, habitualmente llamada “BMW” en la comunidad. El trabajo apareció como preprint a principios de 2020, y en el proceso de revisión por pares ha sido ligeramente revisado como respuesta a las comprobaciones y sugerencias de los expertos consultados por la revista Nature, que finalmente anunció su publicación el mismo 7 de abril, una hora antes del anuncio del primer resultado experimental de Fermilab. El valor obtenido por BMW para g es 2.00233183908(110) – es decir, aμ=0.00116591954(55). La gran novedad es que esto discrepa del valor experimental por sólo 1.5 desviaciones estándar, algo que en física de partículas no se considera estadísticamente significativo. Por lo tanto, de acuerdo con el resultado de BMW, no habría signos de nueva física en el momento magnético del muon. Más aún: el valor difiere del obtenido a partir de los datos de aniquilación electrón-positrón por 2.6 desviaciones estándar, una tensión que ha dejado a la comunidad en un estado de incómoda incertidumbre.
En física, preferimos que los resultados sean replicados por muchos grupos independientes, posiblemente trabajando con distintas metodologías, antes de fiarnos completamente del resultado. Este es, de hecho, el caso del resultado data-driven, para el que varios grupos encuentran desde hace bastante tiempo valores estables ante la incorporación de nuevos datos experimentales, y perfectamente compatibles entre ellos: este es el motivo por el que, en el informe recopilatorio preparado por la comunidad con vistas al nuevo resultado experimental, el valor data-driven fue considerado el de referencia, y se presentó como tal durante el anuncio de Fermilab. En el caso del cálculo en Lattice QCD, por otra parte, es perentorio que otras colaboraciones consigan alcanzar precisiones similares a la de BMW, ya que la complejidad del cálculo es de tal calibre que resulta necesario comprobar de forma independiente todos y cada uno de sus elementos. Sin embargo, sería un error poner este resultado en cuarentena: aunque con errores mayores, los otros resultados de Lattice QCD tienden, como el de BMW, a alinearse con el valor experimental, aumentando la intriga, y la presión para revisar también la metodología data-driven a la luz del nuevo paisaje.
En el lado experimental, además de la ansiosa espera del aumento de la precisión prometido por el experimento de Fermilab, también sería determinante obtener medidas basadas en metodologías distintas. Hay otro experimento planeado en el Japan Proton Accelerator Research Complex (J-PARC), que medirá el momento magnético de muon con un procedimiento totalmente diferente del empleado por BNL/Fermilab. Esto constituirá un paso decisivo para eliminar la posibilidad de errores sistemáticos no detectados. Además, se ha propuesto otro experimento, llamado MuonE, que se podría llevar a cabo en el CERN, y mediría la contribución HVP de manera directa. Semejante medida podría tener un papel decisivo para elucidar la tensión entre el cálculo puramente teórico y la determinación data-driven, en caso de que la misma se mantenga.

El superordenador HAWK, en Stuttgart, uno de los empleados en el cálculo de la colaboración BMW.
[fuente: HLRS]
Si la conclusión de esta resultará ser la confirmación de nueva física, estaríamos hablando de un momento histórico de la física de partículas. El Modelo Estándar ha superado ya los 50 años de edad, enlazando éxitos impresionantes en la descripción de la física de partículas a medida que aumentaban la energía y la precisión de los experimentos. El LHC no ha detectado de momento ninguna partícula no contemplada por el Modelo Estándar, y las señales de posible nueva física han escaseado de manera alarmante… hasta ahora.
¿Qué nueva física podría ser responsable del efecto en el momento magnético del muon? La respuesta a esta pregunta queda de momento muy abierta, y no precisamente por falta de hipótesis – más bien por la abundancia de las mismas. Muchas de ellas podrían explicar el resultado experimental, pero los mecanismos involucrados son incompatibles con otras medidas de precisión en física de partículas, por ejemplo las realizadas en la llamada “física del sabor” – la compleja dinámica de interacción entre partículas pertenecientes a distintas familias del Modelo Estándar. Es muy interesante observar que en los últimos años han surgido discrepancias entre teoría y experimento también en este ámbito, en particular en el estudio de las propiedades de desintegración del quark bottom, y muchas de estas anomalías también implican interacciones en las que interviene el muon. Los esfuerzos de buena parte de la comunidad están ahora mismo dirigidos a explorar las posibles explicaciones simultáneas de los varios efectos, en la esperanza de que proporcionen pistas más sólidas sobre qué modelos podrían resultar más interesantes.
Por supuesto, también es concebible (y las personas más cínicas del campo dirían que probable) que algunas de las discrepancias se expliquen como errores, o que su significatividad estadística se reduzca a medida que se obtengan más datos o se realicen nuevos experimentos, y que la diferencia entre teoría y experimento nunca alcance las mágicas 5 desviaciones estándar. En ese caso, toda esta historia se convertiría en otro capítulo de la galería de éxitos del Modelo Estándar.
Este post fue publicado originalmente en blog QuarkBits por SciLogs-Blogs de ciencia de Investigación y Ciencia.

