Cómo construir tu propio acelerador de partículas… en un PC
Simulaciones numéricas en física de altas energías
Guido Nicotra (fellow de EuroPLEx, Universidad de Bielefeld)

[CERN + pixabay]
Hoy hablamos de esa rama de la Física Teórica conocida como simulación numérica, y trataremos de aplicarla al estudio del plasma de quarks y gluones (que abreviaremos como “QGP”). Pero permítanme algunas palabras introductorias, antes de entrar de lleno en el tema. La Física Teórica se ocupa de la construcción de modelos matemáticos para explicar un conjunto de fenómenos, y sobre todo para proporcionar predicciones verificables, que permitan confirmar o descartar un modelo dado. Si las predicciones son correctas el modelo será aceptado; en caso contrario, habrá que revisarlo, adaptarlo, o directamente descartarlo.
Imaginemos una versión algo novelesca de un Einstein de principios del siglo XX, interesado en buscar un nuevo punto de vista sobre la gravedad. Tras años de duro trabajo, el célebre físico consigue formular una teoría sobre el funcionamiento del espaciotiempo en presencia de una masa: la Teoría de la Relatividad General. Del mismo modo que una tela cuyos bordes se mantienen tensos es deformada por un peso apoyado en su centro, el espaciotiempo hace lo propio en presencia de un cuerpo masivo como una estrella, un planeta, o incluso una vaca (por muy insignificante que pueda parecer en la comparación). No es el lugar para adentrarse en las ecuaciones, pero diremos simplemente que, resolviéndolas para varios casos particulares, Einstein se dio cuenta de que su modelo explicaba observaciones difíciles de comprender, como la precesión del perihelio de Mercurio; o directamente predecía nuevos fenómenos verificables, como el efecto de lente gravitacional, o (indirectamente, a través del trabajo comenzado por Karl Schwarzschild) la existencia de agujeros negros y del efecto de corrimiento al rojo gravitacional asociado a los mismos. El trabajo de la expedición astronómica británica de 1919, dirigida por Arthur Eddington, fue fundamental para empezar a confirmar una de las principales predicciones de la teoría, intentando mostrar que, durante un eclipse solar, era posible ver estrellas que deberían haber permanecido escondidas tras el Sol, lo que hacía manifiesto el fenómeno de lente gravitacional. Desde aquel episodio, cada verificación experimental u observacional de la teoría de Einstein ha confirmado su modelo matemático.
En pocas palabras, ¿qué aprendemos de esta historia? Einstein reelaboró la vieja versión de la gravedad (que pasó de ser una fuerza newtoniana entre dos cuerpos a curvatura del espaciotiempo) y encontró complicadas ecuaciones que la describen; analizando y resolviendo dichas ecuaciones fue descubierta una larga serie de posibles fenómenos hasta entonces desconocidos; mirando hacia arriba, en la inmensidad del Universo, ha sido confirmada la existencia de esos fenómenos.
Volvamos ahora a nuestro punto de partida. Durante el último siglo se ha llevado a cabo un enorme esfuerzo en el campo de la física cuántica hasta llegar a producir la teoría más precisa y completa de la física fundamental jamás realizada: el Modelo Estándar, un conjunto de ecuaciones y modelos matemáticos que describen de manera detallada el mundo microscópico de las partículas elementales. Una de las fronteras actuales de este campo es precisamente el QGP, que ofrece la posibilidad de observar durante un brevísimo período de tiempo las interacciones entre muchas partículas a temperaturas y presiones elevadísimas. Así, mientras en aceleradores de partículas como el LHC del CERN o el RHIC del Brookhaven National Laboratory se hacen colisionar iones pesados para producir las condiciones que permitan generar ese hipotético nuevo estado de la materia, los físicos teóricos atacan las ecuaciones del Modelo Estándar ayudados por superordenadores para tratar de simular la realidad. Existen varios modos para llevar a cabo estos cálculos; aquí describiremos la técnica de simulación de la interacción fundamental fuerte sobre un retículo espaciotemporal, la llamada “Lattice QCD” o Cromodinámica Cuántica en el Retículo.
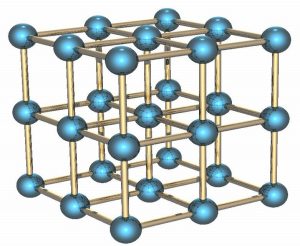
Una versión tridimensional de nuestro espaciotiempo discreto.
El primer paso para formular la teoría en modo adecuado al estudio numérico consiste en colocar el sistema que queremos estudiar en una caja finita (de cuatro dimensiones), haciéndola periódica: cuando alcancemos un lado de la caja apareceremos inmediatamente en el lado opuesto. El segundo paso, también esencial, consiste en evitar el número infinito de grados de libertad necesario para describir partículas que se mueven en un espaciotiempo continuo; para ello, se discretizan las direcciones espaciotemporales, permitiendo a las partículas colocarse sólo en un número finito (aunque enormemente grande) de puntos espaciotemporales, separados por una distancia fija. La geometría del sistema es por lo tanto similar a la de una red cristalina, lo que da origen al término “retículo”. Por último, es necesario describir matemáticamente las partículas, quarks y gluones, con sus correspondientes números cuánticos: los primeros aparecerán como vectores que viven en cada punto espaciotemporal permitido, describiendo los valores de las cargas de color de los quarks; los segundos aparecerán como matrices (las llamadas “link variables”, o “variables de enlace”) que conectan puntos colindantes, transmitiendo cargas de color entre ellos. La forma de las ecuaciones que satisfacen estos vectores y matrices está determinada por la QCD, la parte del Modelo Estándar que describe la interacción fuerte, y fija completamente el comportamiento del sistema una vez que se introducen los valores de las masas de los quarks y la intensidad de la interacción, dada por la llamada constante de acoplamiento fuerte.
Partiendo de una condición inicial arbitraria, el ordenador deberá calcular la interacción de las partículas hasta hacer que el sistema alcance la temperatura deseada para la simulación. Esto significa hacer evolucionar el sistema. Para ello existen varios algoritmos que, de un modo otro, actúan sobre cada variable que representa las partículas. Supongamos, por ejemplo, que queremos cambiar el valor de una cierta variable a través del llamado algoritmo Metropolis. Para ello, generamos un conjunto de valores aleatorios de los correspondientes números cuánticos; si el cambio acerca el sistema a la temperatura deseada será aceptado, mientras que si lo aleja se dejará que sea el azar quien decida si aceptarlo como una fluctuación cuántica permisible, a través de un dado virtual de muchas caras (de nuevo, en forma de números aleatorios) cuyos valores ganadores están determinados por las ecuaciones de la QCD.
Una vez que el sistema ha alcanzado el equilibrio térmico, es posible extraer las medidas: calcular la fuerza de atracción entre quarks (y cómo la misma se reduce cuando se aproxima el umbral de temperatura más allá del cual se forma el QGP), construir mesones (partículas constituidas por una pareja quark-antiquark), o verificar la masa y la vida media del estado fundamental del sistema, son sólo algunas de las muchas posibilidades permitidas por este tipo de simulaciones. Algunas de estas medidas no son directamente comparables con, u observables en, los experimentos, pero no por ello son menos importantes, ya que permiten apuntalar y hacer más sólida la construcción del edificio teórico sobre el que se apoya la interpretación de los resultados experimentales.
Dado que estas simulaciones no son estrictamente reales, ya que se realizan en un espaciotiempo discreto y de tamaño finito, el procedimiento definitivo para extraer la medidas físicas requiere hacer el retículo cada vez más fino (y la caja cada vez mayor), de manera que la distorsión del continuo espaciotemporal infinito disminuya progresivamente hasta volverse irrelevantemente pequeña, un procedimiento conocido como “tomar el límite continuo”. Evidentemente, esta progresión hacia el continuo implica simulaciones cada vez más costosas en términos de tiempo y recursos necesarios. Lo que nos lleva a la última parte de nuestra discusión: la de los límites computacionales a que nos enfrentamos.

El superordenador Summit, en el Oak Ridge National Laboratory.
La simulación de la dinámica de las partículas requiere el cálculo de complicadas integrales sobre un número monstruosamente grande de variables (del orden de un billón, en las mayores simulaciones que se realizan hoy en día). Como parte de ese cálculo, es necesario invertir gigantescas matrices cuadradas (de hasta decenas de miles de millones de columnas). Las propiedades de la interacción fuerte permiten que la evolución de una pequeña parte del sistema durante un tiempo pequeño se puede llevar a cabo ignorando el resto (paralelización de los cálculos), aunque periódicamente es necesario reunir todas las piezas para recomponer la evolución global (necesidad de comunicaciones rápidas). Este potencial para la paralelización permite utilizar los clusters de gran tamaño disponibles en numerosos centros nacionales e internacionales de supercomputación, en simulaciones que alcanzan las decenas de miles de CPUs empleadas en paralelo. Además, las últimas generaciones de algoritmos permiten utilizar GPUs, que al precio de gestionar menores cantidades de memoria permiten realizar los cálculos aún más rápidamente que en las CPUs. Por citar como ejemplo una máquina utilizada en los cálculos de que estamos hablando, el superordenador Summit, construido en 2018 para el Oak Ridge National Laboratory en Tennessee, fue el superordenador más rápido del mundo hasta junio de 2020, gracias a sus 202.752 CPU cores y 27.648 GPUs Nvidia Tesla, que le permiten realizar hasta 200.000 trillones de operaciones por segundo, acompañadas por 250 Petabytes de espacio de archivos. El superordenador Fugaku, recientemente inaugurado en el centro RIKEN de las afueras de Tokyo, alcanza una capacidad total de cálculo unas tres veces mayor.
Estos potentísimos medios, junto a la investigación de algoritmos cada vez más eficientes o la reciente introducción de métodos de optimización basados en machine learning, atacan el primero de los principales problemas de las simulaciones reticulares: el enorme coste computacional necesario. También quedan muchos problemas abiertos, como el altísimo precio de la introducción de las fluctuaciones cuánticas de los quarks, que hacen los integrandos fuertemente oscilatorios y tardaron décadas en poder ser tenidas en cuenta de manera precisa, o las limitaciones de precisión para estudiar la física de los bariones, las partículas compuestas por tres quarks como protones y neutrones.
Quedaría muchísimo por contar sobre las simulaciones de QCD en el retículo, y lo seguiremos haciendo en futuras entradas del blog. La pregunta que nos podemos plantear para concluir es: ¿Cuáles son las ventajas de este método para hacer ciencia? Las simulaciones numéricas son un excelente complemento a los grandes aceleradores de partículas; además, son ciertamente más económicas, requieren instalaciones más modestas, y tienen implicaciones casi inmediatas sobre la vida cotidiana (basta pensar en las consecuencias de la inversión en el desarrollo de sistemas informáticos). No es el método definitivo y quizás nunca lo será, pero es ciertamente un estupendo par de hombros sobre los que subirse para ver más lejos.
Este post fue publicado originalmente en blog QuarkBits por SciLogs-Blogs de ciencia de Investigación y Ciencia.

