New measurement of the muon’s magnetism may hint at physics beyond the Standard Model
by Lucius Bushnaq (EuroPLEx fellow, Trinity College Dublin)
On April 7th of this year, the Fermilab experiment in Chicago announced a new measurement result for the magnetic moment of the muon. It further confirmed a long-standing discrepancy between its theoretically calculated and experimentally measured value, at the level of 4.2 standard deviations, teasing the possibility of new physics outside the current Standard Model of particle physics. However, a different theoretical calculation published on the same day casts some doubt on this possibility.

The muon g-2 experiment at Fermilab (source: Fermilab).
The muon is an elementary particle in our current model of physics. That is to say, it is one of the fundamental building blocks of the universe as we currently understand it. The muon is a particle a lot like the electron. They have the same electric charge and the same quantum spin (a sort of inherent angular momentum). But the muon is about two hundred times heavier than the electron. It is also unstable. Lone muons at rest decay into other particles in just a few microseconds.
The muon’s magnetic moment has been of great interest to physicists for some time. About two decades ago, a then new experiment at Brookhaven National Laboratory (BNL) carried out a measurement of the muon’s magnetic moment to then never before seen precision, and found a discrepancy between the measurement, and what our current overarching model of particle physics, the Standard Model, predicts the magnetic moment of the muon to be. Searches for new fundamental physics broadly fall into two categories. In direct searches, like those carried out at the Large Hadron Collider (LHC), accelerators collide particle beams at enormously high energy densities. Since mass is energy, this allows for the temporary creation of very heavy particles, potentially outside the energy range described by our current physics. The Higgs boson was discovered in this way.
The second type of searches are precision measurements. In quantum field theory, the world is described as different types of quantum fields, corresponding to different elementary particles, which interact with each other. All of these fields are coupled to each other either directly or indirectly, so the mere existence of an additional type of field slightly influences the behaviour of all the others, even at energy ranges in which the corresponding new elementary particle can’t be produced directly.
Thus, another way of detecting new physics is to measure physical quantities extremely precisely, and compare those measurements to theoretical predictions in the Standard Model. If there is a discrepancy between the two, it may be due to the influence of an additional particle outside the Standard Model. Some quantities are predicted to be more sensitive to corrections from new heavy particles than others, making them particularly suitable for this type of search. The magnetic moment of the muon is one such quantity. Thus, the discrepancy detected at BNL attracted a lot of interest.
Experimental measurements always carry some measurement error. Likewise, theoretical predictions carry a prediction error. Calculating physical quantities in quantum field theory is an involved process, and more effort and computer time is needed the greater the accuracy of the result desired.
The size of the difference between the then best theoretically predicted value and the value measured at the BNL experiment was about 3 standard deviations (SD) of the combined experiment-theory error, corresponding to a chance of about one in 400 of detecting a result like this by chance, if there were no new physics at play.
However, the threshold usually required in physics for announcing a new discovery is 5 SD, corresponding to a chance of about one in 1.5 million of the result occurring by chance if the null hypothesis holds.
So, to either confirm the discovery of new physics, or refute the anomaly as a statistical artefact, both more precise measurements, and more precise theoretical predictions of the muon’s magnetic moment were needed.
 The tugboat Miss Katie pushes the barge carrying the Muon g-2 electromagnet in Mississippi (source: Fermilab).
The tugboat Miss Katie pushes the barge carrying the Muon g-2 electromagnet in Mississippi (source: Fermilab).
On the experimental side, the Fermilab experiment was proposed. It uses a design very similar to the BNL experiment. A beam of high speed muons is produced with a particle accelerator, and injected into a magnetic storage ring. Inside the ring’s magnetic field, the muons experience a slight precession, similar to that of a top spinning on a table, with the magnetic field playing the role of gravity. By measuring the frequency of this precession, experimenters can extrapolate what the magnetic moment of the muons must be.
Fermilab actually reuses the same 700-ton, 15 meters wide superconducting storage ring of BNL for this purpose. It was transported from Long Island to Chicago using barges and trucks. Fermilab has now delivered its first results, taken from the data of the experiment’s first run, carried out. More runs will follow, with the next result expected around the summer of 2022. The first run had a measurement error similar to the BNL result, and the magnetic moment it measured was almost identical. By taking the weighted average of both, the total statistical error is decreased. As a number, the current best experimental value for the unitless magnetic moment of the muon (also called the g-factor) is now 2.00233184122(82). The digits in parentheses signify the uncertainty referring to the last two digits of the measurement. The impressive precision achieved is at the level of 4 to 10 billions. Future runs are expected to be more precise, as more data means smaller statistical errors, and potential systematic errors in the experimental setup are brought under better control. The final target of the Fermilab group is a measurement with an error four times smaller than that of the BNL experiment.
On the theory side, precision has also improved in the intervening two decades. The current leading Standard Model prediction for the muon’s magnetic moment is 2.00233183620(86). This brings the significance of the theory-experiment discrepancy up to 4.2 SD (one in 40, 000).
Most of the prediction error stems from the effects that are the hardest to calculate, the so called hadronic contributions, caused by interactions with quark and gluon fields, the carrier particles of the strong force. Specifically, a contribution called the hadronic vacuum polarisation (HVP) is responsible for most of the error on the theoretical prediction. There are essentially two ways of calculating this contribution.
The first way of doing it, is not to do it. Using a mathematical trick, the HVP can be equated with a totally different experimental quantity (the measured fraction of colliding electrons and positrons forming bound states of quarks). By measuring this fraction in completely different experiments, we can determine what the HVP contributing to the muon’s magnetic moment should be.
This data-driven approach is currently still considered the most precise and reliable way of determining the HVP, and thus the gold standard. The value quoted above uses this method. A potential issue with this is that it doesn’t really form the prediction purely from theoretical first principles, but instead involves data from completely unrelated experiments.
In recent years, a second way of calculating the HVP contribution is slowly starting to become competitive: lattice calculations. These discretise space-time into evenly spaced chunks, enabling the direct calculation of the HVP contribution with numerical methods on the world’s fastest supercomputers. Lattice calculations of the HVP have existed for a long time, but they’ve only recently became able to reach precisions comparable to the data-driven method, thanks in good part due to the ever-increasing speed of computing hardware.
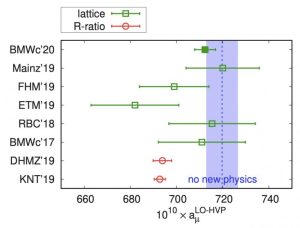
Comparison of results for the hadronic vacuum polarization contribution to the anomalous magnetic moment of the muon (aμ=g-2): estimates based on experimental measurements (blue band), theoretical results from data-driven methods (red) and lattice methods (green) (source: BMW collaboration).
The first, and so far only, lattice result to reach rough parity with the conventional approach was calculated by the Budapest-Marseille-Wuppertal (BMW) collaboration, and first published as a pre-print in early 2020. Using their result, one arrives at a value of 2.00233183908(110) for g. Unlike the value calculated with the data-driven method, it actually agrees with the experimental number inside 1.5 SD, well out of the range of what is considered statistically notable in physics. Thus, according to the BMW result, there is no hint of new physics in the muon’s magnetic moment.
After peer review, the BMW result was finally officially published in Nature on the 7th of April 2021, one hour before the announcement of Fermilab’s first experimental result. Overall, this leaves the particle physics community in a state of uncertainty.
On the theoretical side, the results obtained through the lattice method by BMW and the results obtained through the data-driven method disagree, and this disagreement absolutely needs to be investigated. In physics, we usually prefer results to be replicated by multiple independent groups, working with different methodologies if possible, before we fully trust them. This is why the data-driven calculation was the one used to compare to the experimental result in Fermilab’s official announcement, since it is backed by many cross-checks, and the data used has been collected from many experiments over the decades, and seen successful application in many contexts.
Nevertheless, it absolutely would not do to dismiss BMW. Other lattice groups need to carry out their own calculations at similar precision, to either confirm or refute their result, and the discrepancies between the data-driven and lattice methods need to be investigated piece by piece. If the error turns out to be on the part of BMW, or some broader piece of lattice methodology, the possibility of new physics beckons once more. If it is on the data-driven side, there would not be much reason left to suspect new physical effects at play in the magnetic moment of the muon.
On the experimental side, new, more precise results from Fermilab are awaited eagerly in the years to come. There is also another experiment planned at the Japan Proton Accelerator Research Complex (J-PARC), aiming to measure the muon’s magnetic moment through a method totally different from the setup at BNL and Fermilab, helping to exclude the possibility of unaccounted for systematic errors those experiments.
There is also the MuonE experiment, hopefully to take place at CERN, which would measure the crucial HVP contribution directly, perhaps shedding more light on the discrepancy between the data-driven and lattice results.
 The supercomputer HAWK, in Stuttgart, one of the computing machines used by the collaboration BMW (source: HLRS).
The supercomputer HAWK, in Stuttgart, one of the computing machines used by the collaboration BMW (source: HLRS).
In the end, if the presence of new physics were truly confirmed at more than 5 SD, it would be a monumental occasion in particle physics. The Standard Model is now more than fifty years old, and has been incredibly successful at describing particle physics at the energies our technologies can currently access. New, Beyond-Standard-Model particles failed to show up at the LHC, and ever since then signs of accessible new physics have been thin on the ground.
Which new physics would be at play in the muon’s magnetic moment exactly is still an open question. Not because there aren’t any hypotheses, but because there are still too many of them. Some candidates include supersymmetry, an additional hypothesised symmetry between particles of different spin that would give every Standard Model particle a ”superpartner” particle, and an expanded Higgs sector, consisting of more than one type of Higgs boson. There are also some recent hints at anomalies in flavour-physics experiments that are being examined in this context.
On the other hand, the BMW result might be confirmed by other lattice groups, while some error is discovered in the data-driven methodology. It is also still possible that the theory-experiment discrepancy never reaches the 5 SD threshold after all, and is revealed as a particularly persistent statistical fluctuation as more experimental data comes in. In that case, this whole episode would become just another anecdote to cement the supremacy of the Standard Model in particle physics.
Original story translated with permission from Investigación y Ciencia.

